報(bào)告人: 馬如云、李東升

報(bào)告日期：2020-11-12

報(bào)告時(shí)間：15:00

報(bào)告地點(diǎn)：長安校區(qū) 數(shù)學(xué)與信息科學(xué)學(xué)院學(xué)術(shù)交流廳

主辦單位：陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院

報(bào)告題目一：Global structure of radial positive solutions for a prescribed mean curvature problem

報(bào)告人簡(jiǎn)介：

馬如云，西安電子科技大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院院長。1997年在蘭州大學(xué)獲得博士學(xué)位，同年破格晉升為教授。先后在在美國康涅狄格州立中央大學(xué)（Central Connecticut State University）和澳大利亞昆士蘭大學(xué)（The University of Queensland）做高級(jí)訪問學(xué)者。美國《Math Review》及德國《Zentralblatt Math》評(píng)論員、中國數(shù)學(xué)會(huì)第十二、十三屆理事。主要研究方向是非線性微分方程邊值問題。在J. Funct. Anal., J. Diff. Eqs. Z. Angew Math. Phys.，Proc. Edinburgh Math. Soc.等國際著名學(xué)術(shù)期刊上發(fā)表290余篇論文。入選Elsevier發(fā)布2014-2018年中國高被引學(xué)者榜單。2014-2016年位列數(shù)學(xué)學(xué)科前九名。至2020年4月，其論文已被SCI刊物引用2764次。出版專著3部。近年來，主持國家自然科學(xué)基金項(xiàng)目7項(xiàng)；榮獲甘肅省自然科學(xué)一等獎(jiǎng)1次、甘肅省自然科學(xué)獎(jiǎng)二等獎(jiǎng)4次、甘肅省科技進(jìn)步獎(jiǎng)三等獎(jiǎng)5次、甘肅省高?？萍歼M(jìn)步獎(jiǎng)一等獎(jiǎng)6次；榮獲教育部優(yōu)秀骨干教師、甘肅省名師獎(jiǎng)及甘肅省園丁獎(jiǎng)。2012年起享受國務(wù)院頒發(fā)的政府特殊津貼；2014年榮獲中國僑界貢獻(xiàn)獎(jiǎng)；2015年榮獲秦元?jiǎng)讛?shù)學(xué)獎(jiǎng)；2009年入選甘肅省科技領(lǐng)軍人才第一層次；2009年入選國家新世紀(jì)百千萬人才工程。

報(bào)告簡(jiǎn)介：

We are concerned with the global structure of radial positive solutions of boundary value problem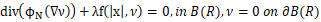，,where,  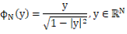, 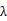is a positive parameter,  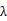and 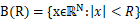 denote the Euclidean norm in. All results, depending on the behavior of nonlinear term near 0, are obtained by using global bifurcation techniques.

報(bào)告題目二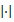： Estimates for Elliptic Equations on  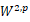Domains

報(bào)告人簡(jiǎn)介：李東升，西安交通大學(xué)數(shù)學(xué)系教授，博士生導(dǎo)師。陜西省數(shù)學(xué)會(huì)常務(wù)理事兼副秘書長。長期從事偏微分方程正則性理論方面的研究，主要成果有：系統(tǒng)地給出使得橢圓（拋物）方程解在邊界可微的最優(yōu)區(qū)域邊界幾何條件；在擬區(qū)域上得到方程的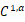估計(jì)，對(duì)于四階方程，允許方程系數(shù)在穿過一個(gè)Reifenberg型曲面時(shí)有跳躍；推廣了Caffarelli完全非線性方程的估計(jì)，并給出斜邊解條件下解及其導(dǎo)數(shù)的Holder估計(jì)等。曾先后多次訪問美國愛荷華大學(xué)、明尼蘇達(dá)大學(xué)、普林斯頓大學(xué)等多所國際著名高校。目前在Adv. Math., Arch. Ration. Mech. Anal., J. Funct. Anal., J. Math. Pure AppL.,Cal.Var.PDE., J. Diff.l Eqs.等國際著名學(xué)術(shù)期刊發(fā)表科研論文60余篇；主持6項(xiàng)國家自然科學(xué)基金；是“三秦人才津貼”獲得者，以及陜西省優(yōu)秀博士論文指導(dǎo)教師獲得者；獲陜西省教育廳科技一等獎(jiǎng)一項(xiàng)，教育部科技進(jìn)步二等獎(jiǎng)一項(xiàng)，陜西省科技進(jìn)步二等獎(jiǎng)一項(xiàng)。

報(bào)告簡(jiǎn)介：

The classical 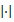estimates for elliptic equations are established on domains. We will extend the estimates on  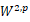domains. Both the Whitney cover lemma and the Vitali cover lemma will be used. By the Whitney cover lemma, we will give a decay rate of the distribution of 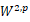and then using the Vitali cover lemma, we will accelerate the decay. In this talk, we will also review the developing of estimates for elliptic equations.